隨著人工智慧持續發展、在不同商業場景中的數據量持續上升，行銷策略的制定與執行變得更加科學化與數據導向，我在先前的文章【商業分析】數據導向之行銷策略：解構數據關聯性與價值 探討了數據的類型以及個別的分析價值，而在這篇文章，我們將聚焦於機器學習演算法，以行銷領域的核心理論：STP 理論為基礎，探討在市場區隔、受眾選擇與品牌定位之商業場景下機器學習可以如何優化策略效益。

本文架構

一、行銷 STP 理論之概念以及策略執行難點

二、Segmentation：以分群模型區隔不同客群（K-Means Clustering）

三、Targeting：以分類模型，瞄準高潛力客群（Logistic Regression）

四、Positioning：以降維分析進行品牌定位重塑（Principal Components Analysis）

五、從模型到價值，機器學習驅動行銷 STP 的未來

一、行銷 STP 理論之概念以及策略執行難點

（一）STP 理論的核心概念

「當你想討好每個人，最後反而會一無是處」，這是 STP 理論的核心，STP 理論主張市場不同客群具有異質性，企業需要先定義欲瞄準的目標客群，再制定相應的行銷組合（即行銷 4P）以對應目標客群的需求。而 STP 理論建議企業可以透過市場區隔（Segmentation）、瞄準目標客群（Targeting）以及定位（Positioning）這三個步驟以達到前述的策略效果。

以下是三個步驟分別的內容：

• Segmentation：將市場透過不同維度將客群切分開來，在切分市場可以運用的維度包含人口統計變數、地理變數、行為變數、心理變數等。個人認為一個好的市場區隔最好能滿足以下特性，分別是市場區隔要具有足量性，市場規模需要夠大、要能夠凸顯區隔之間的不同點、要能夠指引策略方向。
• Targeting：根據市場區隔所區分的不同客群，選擇欲瞄準的目標客群，選擇目標客群的方式可以不限於單一指標，包含市場規模大小、成長性、開發可行性等。
• Positioning：根據選擇之目標客群設定品牌定位，可以理解為品牌呈現在客戶面前的形象。

（二）STP 理論之策略執行難點

STP 理論實際上在執行上會有什麼困難呢？首先在 Segmentation ，傳統的區隔方式較難以多維的方式區分市場，區分之顆粒度會受到限制、缺乏數據基礎去衡量區隔間的差異與區隔內的差異，來決定市場區隔的細分程度等；而在 Targeting 上，若無數據與演算法的協助，將很難精準衡量每個目標客群對於企業產品或服務的採用機率高低，較難精準選擇客群；最後在 Positioning 上，衡量品牌定位的維度眾多，如何聚焦影響品牌定位的關鍵因素以及以量化方式評估相對於競爭對手的定位便是一個重要的難題。

二、Segmentation：以分群模型區隔不同客群（K-means Clustering）

首先先來討論機器學習在市場區隔的應用，這邊主要討論的是分群模型 K-Means Clustering，會先從分群模型應用在市場區隔的策略效益開始討論，再來說明 K-Means Clustering 的演算法以及超參數的設定。

（一）分群模型應用在市場區隔的策略效益

傳統的市場區隔大多以二維作為區分，透過分群模型可以跳脫這個限制，處理多維的分群問題，如此一來可以捕捉更細緻的消費者行為。此外，相較於主觀的市場區隔，分群模型提供了更量化的方式去評估區隔間與區隔內的差異。

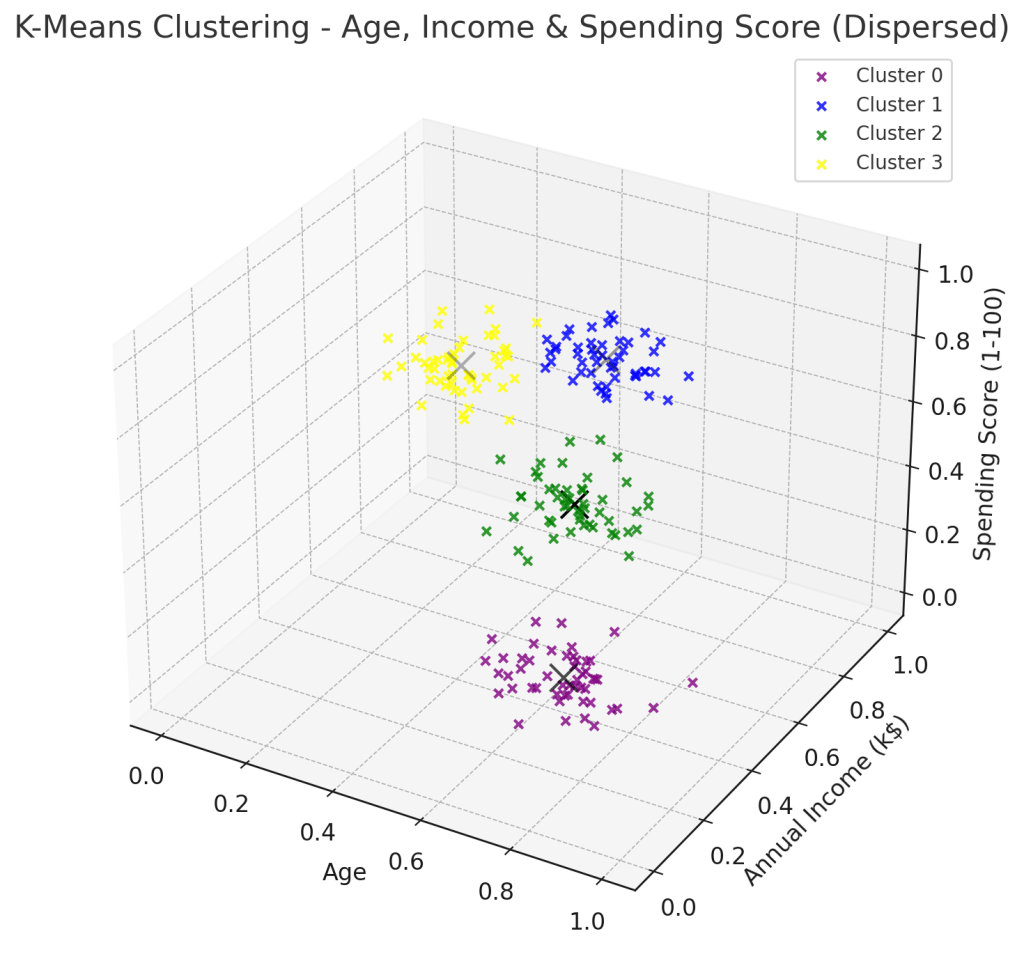
（二）機器學習演算法介紹：K-Means Clustering

模型直覺

K-Means 是一種常見的非監督式學習（unsupervised learning）分群演算法，主要用於將數據分成 k 個不同的群組，透過計算每個數據點距離群心的位置最小化群內彼此的誤差並最大化群組之間的差異。

演算法

K-Means Clustering 演算主要步驟如下：

1. 初始化：隨機選擇 k 個初始群心
2. 分配樣本：透過計算歐幾里得距離（直線距離）將每個數據點指派到距離最近的群心，形成 k 個群集
3. 更新群心：透過取該群內所有點的平均值，重新計算每個群集的中心點，數學表示如下：

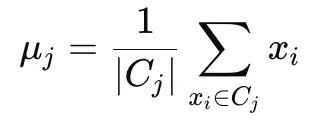
4. 重複步驟 2 和 3，直到群心不再變動或變動極小

透過這樣的方式，K-Means Clustering 可以最小化群內之間的變異，具體而言就是最小化群內誤差平方和（Within-Cluster Sum of Squares, WCSS），這也就是機器學習模型以量化方式評估群內變異的方式，相較於傳統主觀式的市場區隔更加科學化。以數學方式去表示 K-Means Clustering 的目標函數可以寫成如下的方式，便是最小化每個數據點與群心得距離平方和。

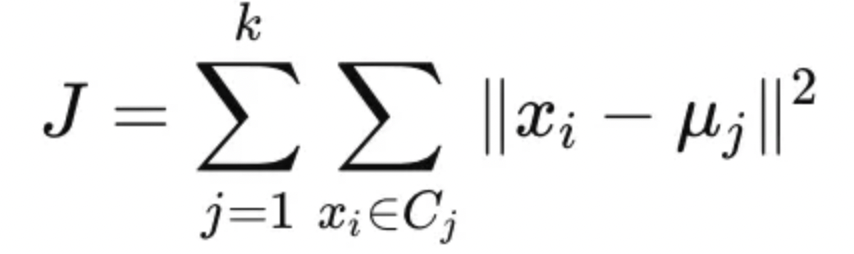
分群群數 K 的設定

在 K-Means Clustering 當中，K 是需要預先指派的超參數，也就是一開始就要先決定要將數據分為幾群，雖然將 K 訂得越大 WCSS 肯定就會變得更小，但這樣便有可能過度分群，反而不利後續的客群瞄準、或是導致單一客群市場規模過於狹小。而在決定超參數 K 要如何設定時，可以參考肘點法去設定，所謂的肘點法是將 WCSS 與 K（分群數量）的關係會製成圖，找到 WCSS 趨於緩和的轉折點（也就是所謂的肘點）作為 K 的設定值。

應用情境與限制

分群模型有許多種類，K-Means Clustering 適合以重心作為中心點圓形分部，在這種情況下分群效果較好，如果遇到不同種類的分佈，就必須考慮使用其他種類的分群模型較為適合。此外，由於每次都是隨機選擇 k 個初始群心作為演算法的第一步，K-Means Clustering 每次產生的分群結果可能不盡相同，這時便需要重複多跑幾次，比較不同的分群方式所以對應的損失函數大小，挑選出最適合的分群方式。

三、Targeting：以分類模型，瞄準高潛力客群（Logistic Regression）

（一）分類模型應用在客群瞄準的策略效益

傳統在瞄準目標客群時，多偏向主觀的判斷該客群採用的機率高低，作為客群開發可行性的參考。而如果採用分類模型，將可以計算出該客群採用企業產品或服務的機率，做到精準瞄準甚至是個人化行銷。

（二）機器學習演算法介紹：Logistic Regression（邏輯回歸）

模型直覺

Logistic Regression（邏輯回歸）雖然名字中有回歸，但並不算是回歸方法，而是屬於監督式學習中的分類方法，Logistic Regression 是透過學習某件事發的機率，並透過與閾值（Threshold）來進行分類。

演算法

邏輯回歸的核心在於計算出資料 X 屬於某類別的機率，進而進行分類，以數學表示其演算法便是如下的式子：

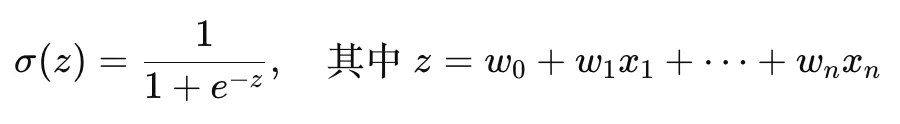
可以看到 Logistic Regression 類似線性回歸，將權重向量乘上資料，再加上誤差項（W0），然而 Logistic Regression 還會透過 Sigmoid 函數（上述數學式的 σ(z)）去轉換原先的輸出成為機率，而這個機率便是資料點 X 屬於特定類別的機率，若高於預先設定的閾值（通常設定為 0.5）便判定為該類別。

Logistic Regression 在進行學習時，會透過將邏輯損失函數最小化來找到最適合的參數 W，其損失函數為如下所示：

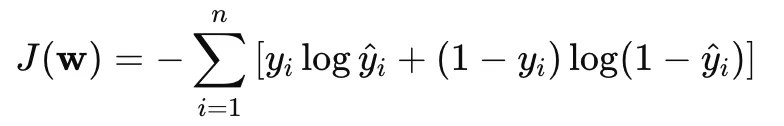
這個損失函數來自於最大化對數似然函數（Maximum Likelihood Estimation, MLE），也可以稱為交叉熵損失函數，可以衡量模型預測的機率分佈與實際標籤分佈的接近程度，當預測錯誤時，對應的損失會較大。

直覺地來看這個損失函數，當 y 實際為 1 時，若預測值 y 也為 1，則損失函數為 0，而若預測錯誤則損失函數的值會極大，因此以這個函數作為目標函數去最小化它可以有效促使模型降低預測錯誤的機率。

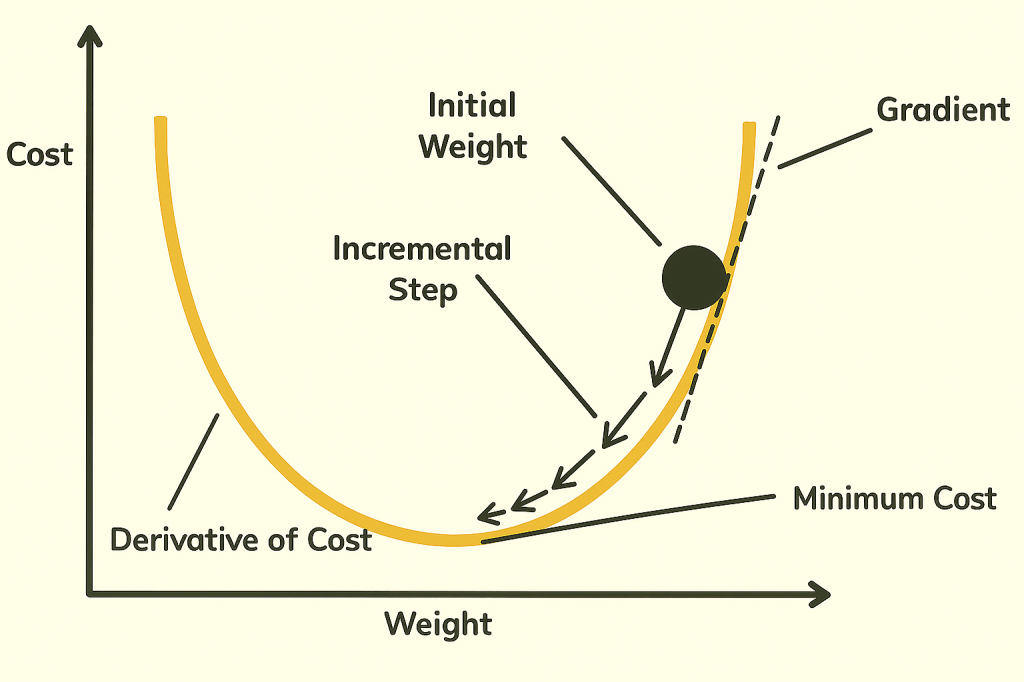
而具體而言如何最小化損失函數呢？我們通常會使用梯度下降法 (Gradient Descent) 找出一組參數 w，來最小化損失函數。梯度下降法可以用來尋找函數的最小值，特別適用於機器學習的損失函數最小化問題，其基本概念是：

1. 計算損失函數的梯度（偏導數的概念，為函數改變的切線方向），找到損失函數最陡峭的下降方向。
2. 沿著梯度方向移動一小步（學習率 α 控制步長），逐步逼近最小值。

如下方的數學式所示，每次 w 都會以梯度的反方向去進行同步更新，而更新的速度則由學習率 α 控制。

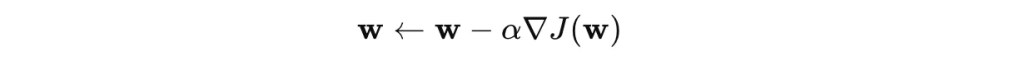
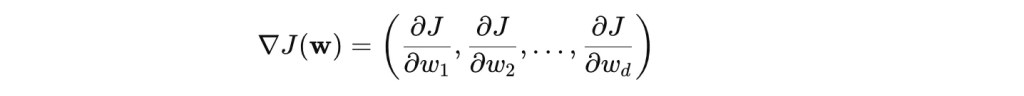
梯度下降法有一個使用上的限制，那便是目標函數必須為凸函數 (Convex function)，否則找到的最小值可能不是 Global minimum 而是 Local minimum。

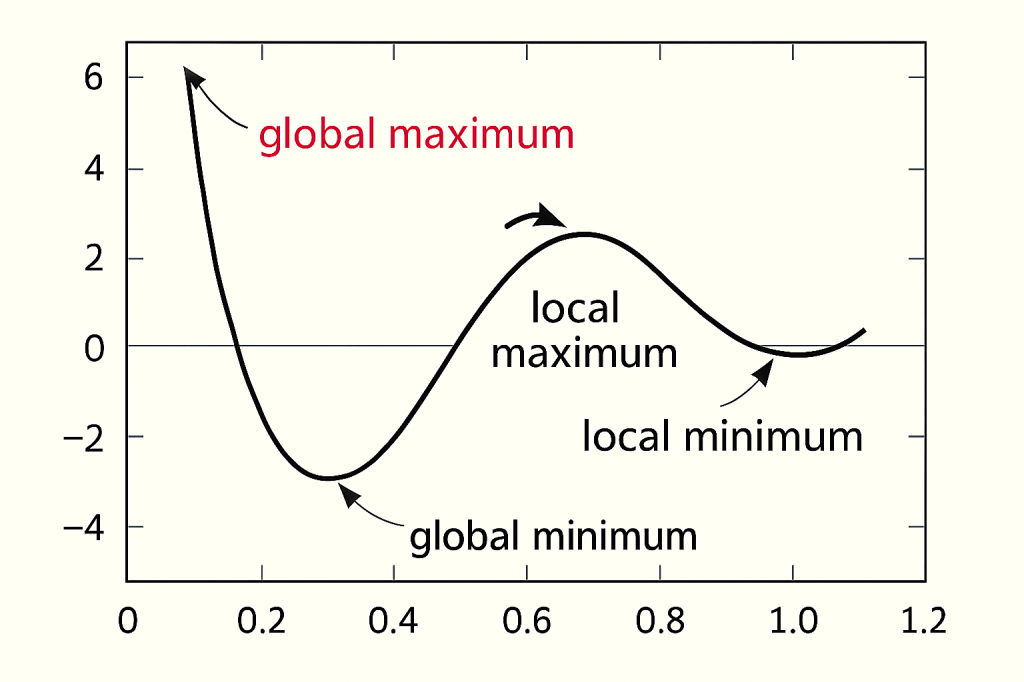
學習率 α 的設定

學習率 α 的設定會影響模型學習的效率與精確度，若學習率設定的過小，則模型將會花過多時間收斂至最小值，若學習率設定的過大，則有可能會使模型無法收斂至最小值，導致錯誤。在學習率的設定上，可以由小至大逐步調整學習率，觀察梯度的變化方向以及損失函數是否逐步下降，來決定學習率至高可以調整到多少。

應用情境與限制

Logistic regression 透過建立線性的決策邊界進行分類，若資料不適合透過線性的決策邊界來分類，則分類效果將不好，此時可以透過 Feature mapping 來修改 Logisitc regression 的決策邊界至多維，或著採用其他的分類模型。此外，也要注意模型是否出現 overfitting（過度擬合），若出現過度擬合則模型的一般化效果變不好。

四、Positioning：以降維分析進行品牌定位重塑（Principal Components Analysis）

（一）降維分析應用在品牌定位之策略效益

在討論品牌定位時，常會使用知覺定位圖（Perceptual Map）來進行分析，然而衡量品牌定位的維度眾多，使用機器學習的降維分析方式可以收斂影響品牌定位的維度以制定進一步的行銷策略。

（二）機器學習演算法介紹：Principal Components Analysis（主成分分析）

模型直覺

Principal Components Analysis (PCA) 是一種降維方法，它的目標是將高維數據投影到較低維度的空間，同時最大程度保留原始數據的變異性，這個方法能夠幫助我們重新以不同的維度（也就是稍後會提到的主成份）去詮釋資料以提取洞察。

PCA 的核心思想是找到數據中變異性最大的方向（即資料最分散的方向），沿著這些方向建立一組彼此正交的主成分，用較少的主成分來近似原始數據，以達到降維效果。

演算法

PCA 的演算法步驟如下，接下來將一步一步展開：

1. 將數據標準化，確保不同尺度的變數對 PCA 有相同影響
2. 計算共變異數矩陣
3. 計算特徵值 (eigenvalues) 與特徵向量 (eigenvectors)
4. 選擇 k 個主成分

在數據標準化之後，就會先計算共變異數矩陣，這是用於之後特徵分解的基礎，共變異數矩陣是一個對稱矩陣，對角線元素是變數的方差，非對角線元素是變數之間的共變異數，具體如下。

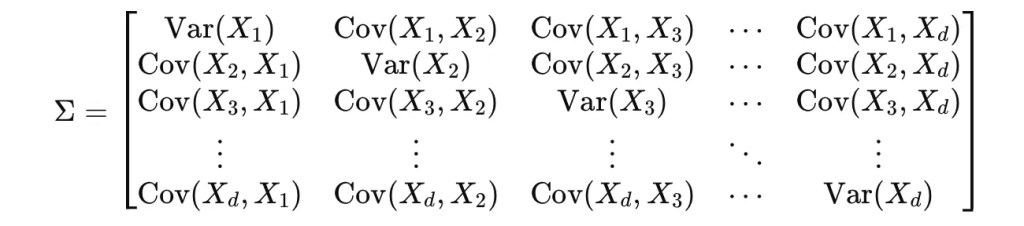
有了共變異數矩陣後，就可以進行特徵分解，特徵值分解便是計算共變異數矩陣的特徵值 (eigenvalues) 與特徵向量 (eigenvectors)，亦即將共變異數矩陣分解為以下的形式。在以下的數學式中，v 為矩陣 A 的特徵向量（eigenvector)，而 λ 為對應的特徵值（eigenvalue）：

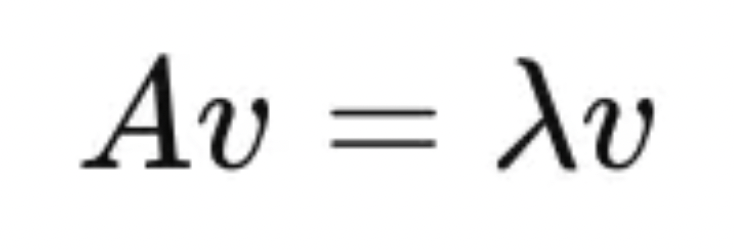
不同的特徵向量代表不同主成分，而對應的特徵值則代表該主成分能夠反映資料的變異性有多高，也可以說是主成分的重要性。因此會將特徵值按從大到小排序，並選擇前 k 個對應的特徵向量作為新的座標軸，即前 k 個主成分，如此一來便可以只用這 k 個主成分來近似原始數據。

主成分數量 k 的選擇方式

通常會以特徵值來計算累計貢獻率，進而決定要選擇多少主成分進行分析，如果累積貢獻率能夠達到 80% 以上，則代表降維後的呈現方式仍然能夠反應資料原始的狀況。累計貢獻率的分母是 n 個特徵值的加總，而分子則是前 k 個特徵值的加總，具體如下：

主成分的解讀方式與後續應用

主成分選擇之後，重要的還是如何去解讀主成分，才能夠產生商業上的洞察，否則主成分本身就僅會是數個能夠呈現原始資料變異的向量。而若要能夠解釋主成分所代表的意義，則可以從主成分負荷量 (Princiapl Component Loading) 下手，了解原始變數對該主成分的貢獻度有多少，越高係數的變數代表對該主成分影響大，如此一來便可以了解該主成分涵蓋哪些變數。

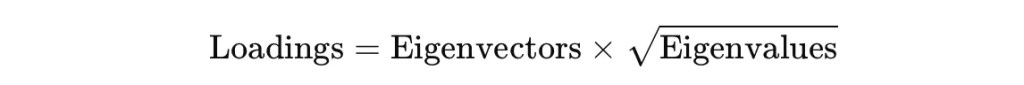
如上述的數學式，主成分負荷量可以透過對特徵值開根號再乘上特徵向量去計算。

五、從模型到價值，機器學習驅動行銷 STP 的未來

隨著機器學習日益滲透進行銷決策流程，企業在導入這些技術於 STP 模型時，必須同時關注「模型效能」與「組織整合」兩大層面。若缺乏對模型可用性的全面評估與對轉型風險的理解，機器學習再先進也可能淪為無法落地的實驗性專案。因此，衡量一個 STP 機器學習系統的成功，不僅是技術是否精準，更在於它是否真正幫助企業理解市場、強化決策、創造價值。

首先，在模型效能評估層面，我們需透過量化指標來檢視其在實務中的可行性。以 Targeting 的分類模型為例，F1-score 可平衡精準率與召回率，協助評估在廣告投放中能否「找到對的人」。對於如定價預測等回歸任務，R² 決定係數與均方誤差（MSE） 能幫助企業判斷模型是否足以支持價格策略與銷售預測。同時，對於監督式學習的機器學習演算法，也需要衡量該模型是否有過度擬合的現象，可以透過正則化等方式避免並透過 Cross Validation 的方式進行衡量。

然而，導入機器學習模型不只是依靠演算法，更關鍵的是組織是否有能力駕馭它。最常見的挑戰包括：資料品質不足（如跨通路數據斷裂、標記錯誤）、模型透明度不足導致難以信任（尤其對非技術團隊而言），以及組織內部缺乏跨部門整合與數據文化，使得模型無法轉化為實際行動。此外，若僅把機器學習當作一次性的行銷實驗，忽略持續性更新與策略整合，往往會淪為「只看到準確率，沒看到影響力」的窘境。

綜結而言，機器學習能提升 STP 模型的精準性與效率，但技術只是手段，關鍵仍在於企業是否能建立清晰的評估機制、擁抱資料文化、並擁有一套將洞察轉化為行動的能力。在這樣的轉型路上，機器學習不是終點，而是引領行銷進化的核心驅動力。

以上就是本次商業分析的議題與分析，希望以上內容能幫助到你！如果喜歡的話，歡迎進一步與我交流～